This project aims to design an automated traffic signal control system that dynamically adjust traffic lights based on real traffic flow, with focused priority on the movement of emergency vehicles. #ReinforcementLearning

The main idea is to reduce the overall wait time for the emergency vehicles travelling from one to another destination. To achieve this task, we are using Reinforcement Learning to train a traffic signal controller in a simulated environment (SUMO-RL). Our code and model is available here.

We trained the agent with various algorithms (i.e. SARSA, Q-Learning, DQN, Double DQN and A2C) and compared their performance. The project is an enhancement of an existing work - Diagnosing Reinforcement Learning for Traffic Signal Control

Comparison

Fixed TL Results

The traffic light follows a static program with a cycle: 42 seconds green for one direction (likely North-South based on connections), 2 seconds yellow, 42 seconds green for the other direction, and 2 seconds yellow.

SARSA Results

• Since the max queue length for the environment = 20, so the state space can get really big. To address this we quantized the queue length vector into 4 regions: [0-5(Low 1), 5-10(Low 2), 10-15(High 1), 15-20(High 2)]
• Phase and Emergency vehicle lane was also changed to cardinal numbers.
• With this the new state space is of size [0-3, 0-3, 0-3, 0-3, 0-3, 0-4] = 5120
• The agent was trained for 200 episodes with epsilon decay and discount factor of 0.99 The agent performed better than the fixed network, but the TL logic was heavily imbalanced toward one lane and the model failed to converge.

QLearning Results

• We followed the similar state space as SARSA
• The agent was trained for 100 episodes with epsilon decay and discount factor of 0.9 With QL, the agent performed better than SARSA in terms of wait time. Moreover, the agent was able to solve for at least one of lanes completely.

DQN Results

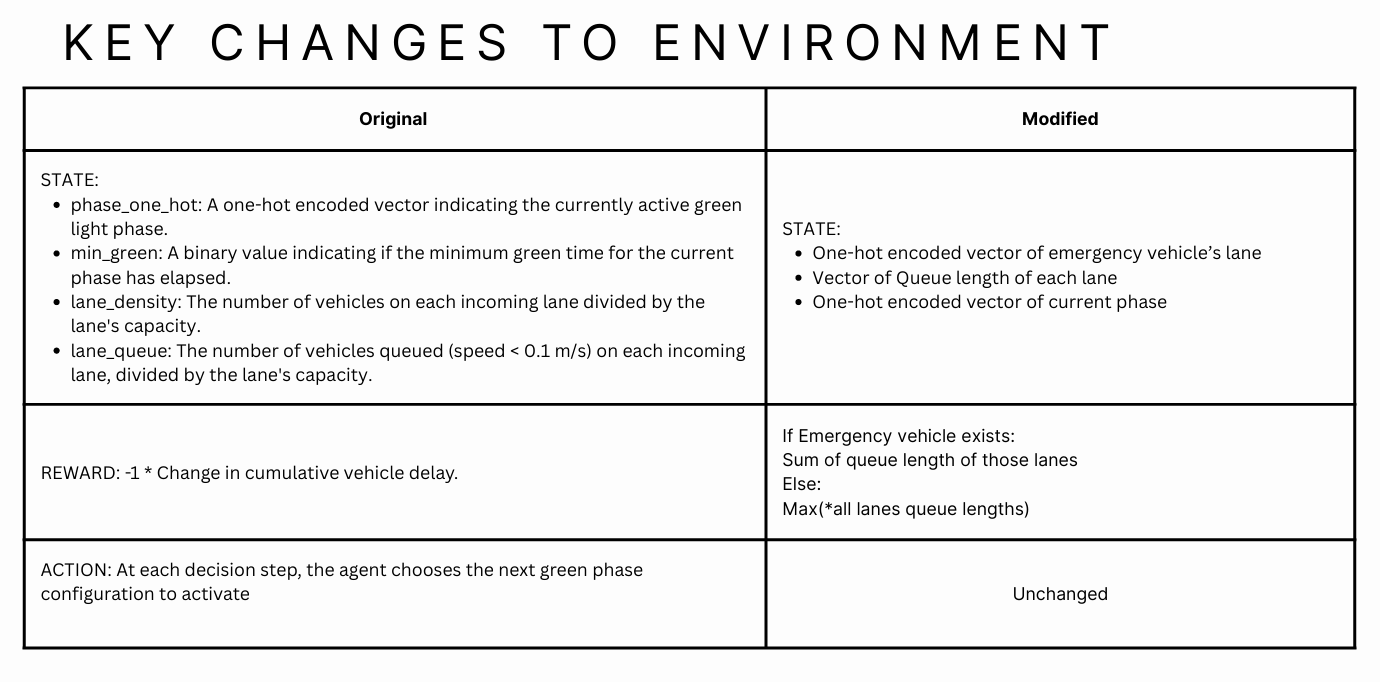
• Observation: Normalized queue lengths of each lanes + one-hot-encoded phases + emergency vehicles boolean value represented as 0 and 1.
• Action: 0 to stay in current phase, 1 to go in next phase.
• Reward: -1 * (max(n_t, w_t)) or sum of queue lengths where emergency vehicles exists.
• Buffer size = 500
• Batch size = 32
• Episodes 200
• Learning rate = 0.01
• Discount factor = 0.99
• Network: 3 layers with 128 neurons, 12 input size, 2 output

DDQN Results

• Observation: Normalized queue lengths of each lanes + one-hot-encoded phases + emergency vehicles boolean value represented as 0 and 1.
• Action: 0 to stay in current phase, 1 to go in next phase.
• Reward: -1 * (max(n_t, w_t)) or sum of queue lengths where emergency vehicles exists.
• Buffer size = 500
• Batch size = 32
• Episodes 200
• Learning rate = 0.01
• Discount factor = 0.99
• Network: 3 layers with 128 neurons, 12 input size, 2 output

Key Observations

• Reward shaping was the key. Only using summation of queue length was not enough, the model was gaming the rewards by minimizing length for 1 lane and keeping the other lane full.
• Simplifying phases helped. Granular control on phases led to higher converge times and often it is unrealistic to keep only 1 lane open at a time.
• Episode length vs number of episodes. We trained the model on shorter episodes lengths to emphasize quicker model updates and then tested it on longer episodes. This showed us the fastest convergence.

Reward Hacking

We see here that model learns to minimize the penalty by letting 1 lane wait for longer times and keeping the other lane open.